数学学院“小数苗”支教团成员 徐翔宇

1月29日一早，我和山东大学“小数苗”支教调研团的陈政润、郎咸宇同学便来到了港沟街道景和山庄社区青年之家，展开了新一天的数学科普课堂。

上午九时，我们准时来到了教室，同学们已经早早到教室做好了上课准备，陈政润将教具“汉诺塔”发给了同学们，开始今天的课程。随着陈政润的介绍，同学们了解到汉诺塔是几个大小不同的圆环在三根柱子之间转移的趣味游戏，一次只能移动一个并且小的圆环必须要在大的圆环上面，需要将原本叠在一根柱子上的圆环转移到另一根圆环上去。

陈政润让同学们先自己动手尝试三阶与四阶的汉诺塔问题，并拿出一张白纸记录自己是如何一步步迭代并最终完成转移的。他提醒大家可以用前几节课学到的搜索算法，按一定顺序进行尝试与枚举，看看如何能又快又准地完成转移。

在大家全身心投入、积极尝试的过程中，陈政润发现了一个女生似乎发现了不同阶数汉诺塔当中的规律。于是陈政润鼓励她在白板上展示出自己的发现，在陈政润的指引下，她在写下三四阶汉诺塔的最少步骤的同时，还写下了五阶问题的最优解。陈政润将这一部分现实问题抽象成数学模型，用数字表示每一步的操作。并引导同学们每增加一维汉诺塔问题，都可以由原来维数的答案稍微变形得到，引导同学们找到n阶汉诺塔问题的最短步骤是2^n-1次。

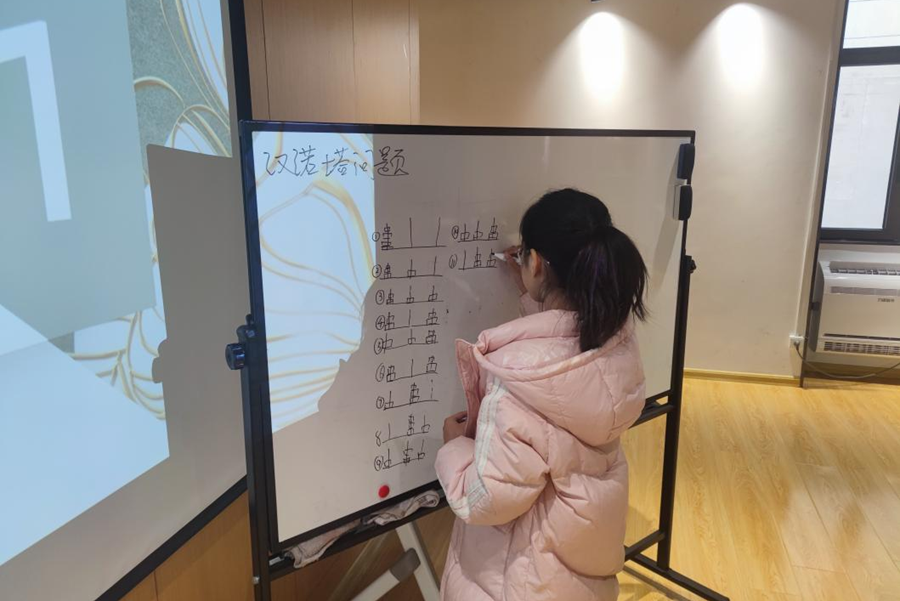
通过汉诺塔问题，陈政润自然地引出了递归的概念，“递”就是传递，“归”就是回归，所谓“递归”就是将当前问题的解回归到维数稍小问题的解，然后逐层传递下去，进而得到答案。陈政润拿出了角型密铺的例子，让同学们在8*8的格子种铺满三角块，8*8不好解决可以先解决4*4的问题，4*4的问题又可以先通过2*2的问题解决。一步步递归便解决了最初的问题。

下午的课程由郎咸宇同学主讲。下午14时，郎咸宇从数列的定义引入，引导同学们通过观察找到等差数列等差的性质，然后根据数列的递推公式，一点一点推导数列的通项公式，进一步强调了递推与递归的观念。

今天的最后一个话题仍然围绕递推与递归展开——来自组合数当中的递归问题。通过枚举法计算3个当中选2两个，3个当中选1个的问题，进而推广到在4个当中选择，在5个当中选择。不过这里的变化在于，今天早些时候学习的递推递归都是维数缩减之后仍然是求解一个问题，但是组合数是求解两个问题，而其中的思想是不变的。郎咸宇耐心地书写着求解组合数问题的递推过程与思路，将全部的组合数按行写在黑板上，有一个小女生抢答出了“这是杨辉三角”。郎咸宇便顺着她，继续讲解，指出杨辉三角的每个数字恰好就是对应的组合数，而杨辉三角的画法又恰恰是组合数的递推公式。

随着大家对于递推递归理解的逐步加深，对杨辉三角与组合数问题的逐步理解，今天的课程也暂告一段落。虽然本次的数学科普讲堂结束了，但无论是同学们还是数学专业的我们，探索数学探索未知的脚步将不会停歇！我们将始终秉持那颗细致、严谨的心为国家作出数学人的贡献！